| Definitions | x f y, (i =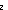 j), j),  , x:A , x:A  B(x), rel_exp(T;R;n), f(a), type List, B(x), rel_exp(T;R;n), f(a), type List,  , s = t, rel-path-between(T;R;x;y;L), x:A , s = t, rel-path-between(T;R;x;y;L), x:A  B(x), P & Q, B(x), P & Q,  x:A. B(x), P x:A. B(x), P    Q, Q,  x:A. B(x), Type, x:A. B(x), Type,  , {x:A| B(x)} , t , {x:A| B(x)} , t  T, A T, A  B, i B, i 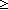 j , P j , P   Q, False, Q, False,  A, #$n, -n, n+m, n - m, a < b, Void, P A, #$n, -n, n+m, n - m, a < b, Void, P   Q, ||as||, Q, ||as||,  b, last(L), rel-path(R;L), hd(l), <a, b>, b, last(L), rel-path(R;L), hd(l), <a, b>,  , A c , A c B, [], [car / cdr], i <z j, i B, [], [car / cdr], i <z j, i  z j, l[i], {i..j z j, l[i], {i..j }, i }, i  j < k, ff, j < k, ff,   b, tt, x =a y, null(as), a < b, tt, x =a y, null(as), a < b, a < b, a < b, [d] b, [d] , p , p    q, p q, p   q, p q, p   q, Unit, left + right, q, Unit, left + right,  x.A(x), A List x.A(x), A List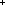 , , 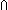 x:A.B(x), Top, S x:A.B(x), Top, S  T, True T, True |